Theorem: The projections of any vector
We now arrive finally at the main desired result for this section:
Theorem: The projections of any vector
![]() onto any orthogonal basis set
for
onto any orthogonal basis set
for
![]() can be summed to reconstruct
can be summed to reconstruct ![]() exactly.
exactly.
Proof: Let
![]() denote any orthogonal basis set for
denote any orthogonal basis set for
![]() .
Then since
.
Then since ![]() is in the space spanned by these vectors, we have
is in the space spanned by these vectors, we have
(using the linearity of the projection operator which follows from linearity of the inner product in its first argument). Since the basis vectors are orthogonal, the projection of
![$\displaystyle {\bf P}_{\underline{s}_k}(\underline{s}_l) \isdef
\frac{\left<\underline{s}_l,\underline{s}_k\right>}{\left\Vert\,\underline{s}_k\,\right\Vert^2}\underline{s}_k
= \left\{\begin{array}{ll}
\underline{0}, & l\neq k \\ [5pt]
\underline{s}_k, & l=k. \\
\end{array} \right.
$](img966.png)
We therefore obtain
Therefore, the sum of projections onto the vectors
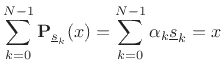
by Eq.(5.3).