In discrete-time audio processing, such as we normally do on a computer,
we work with samples of continuous-time signals. Let ![]() denote the sampling rate in Hz. For audio, we typically have
denote the sampling rate in Hz. For audio, we typically have ![]() kHz, since the audio band nominally extends to
kHz, since the audio band nominally extends to ![]() kHz. For compact
discs (CDs),
kHz. For compact
discs (CDs), ![]() kHz,
while for digital audio tape (DAT),
kHz,
while for digital audio tape (DAT), ![]() kHz.
kHz.
Let
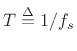 denote the sampling interval in seconds. Then to
convert from continuous to discrete time, we replace
denote the sampling interval in seconds. Then to
convert from continuous to discrete time, we replace ![]() by
by ![]() , where
, where ![]() is an integer interpreted as the sample number.
is an integer interpreted as the sample number.
The sampled generalized complex sinusoid is then
![\begin{eqnarray*}
y(nT) &\isdef & \left.{\cal A}\,e^{st}\right\vert _{t=nT}\\
&=& {\cal A}e^{s n T} = {\cal A}\left[e^{sT}\right]^n \\
&\isdef & A e^{j\phi} e^{(\sigma+j\omega) nT} \\
&=& A e^{\sigma nT} \left[\cos(\omega nT + \phi) + j\sin(\omega nT + \phi)\right] \\
&=& A \left[e^{\sigma T}\right]^n
\left[\cos(\omega nT + \phi) + j\sin(\omega nT + \phi)\right].
\end{eqnarray*}](img603.png)
Thus, the sampled case consists of a sampled complex sinusoid
multiplied by a sampled exponential envelope
![]() .
.