Projection onto Linearly Dependent Vectors

Now consider another example:

$$\begin{eqnarray*} \underline{s}_0 &\isdef & [1,1], \\ \underline{s}_1 &\isdef & [-1,-1]. \end{eqnarray*}$$

The projections of $x=[x_0,x_1]$ onto these vectors are

$$\begin{eqnarray*} {\bf P}_{\underline{s}_0}(x) &=& \frac{x_0 + x_1}{2}\underline{s}_0, \\ {\bf P}_{\underline{s}_1}(x) &=& -\frac{x_0 + x_1}{2}\underline{s}_1. \end{eqnarray*}$$

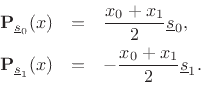
The sum of the projections is

$$\begin{eqnarray*} {\bf P}_{\underline{s}_0}(x) + {\bf P}_{\underline{s}_1}(x) &=& \frac{x_0 + x_1}{2}\underline{s}_0 - \frac{x_0 + x_1}{2}\underline{s}_1 \\ &\isdef & \frac{x_0 + x_1}{2}(1,1) - \frac{x_0 + x_1}{2} (-1,-1) \\ &=& \left(x_0+x_1,x_0+x_1\right) \neq x. \end{eqnarray*}$$

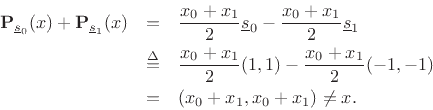
Something went wrong, but what? It turns out that a set of $N$ vectors can be used to reconstruct an arbitrary vector in $\mathbb{C}^N$ from its projections only if they are linearly independent. In general, a set of vectors is linearly independent if none of them can be expressed as a linear combination of the others in the set. What this means intuitively is that they must ``point in different directions'' in $N$ -space. In this example $s_1 = - s_0$ so that they lie along the same line in $2$ -space. As a result, they are linearly dependent: one is a linear combination of the other ( $s_1 = (-1)s_0$ ).