Definition: The frequency response of an LTI filter may be defined as the Fourier transform of its impulse response. In particular, for finite, discrete-time signals
Definition: The frequency response of an LTI filter may be defined
as the Fourier transform of its impulse response. In particular, for
finite, discrete-time signals
![]() , the sampled frequency
response may be defined as
, the sampled frequency
response may be defined as
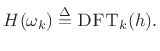
The complete (continuous) frequency response is defined using the DTFT (see §B.1), i.e.,
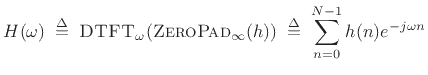
where the summation limits are truncated to