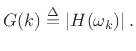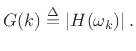Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Definition: The amplitude response of a filter is defined as
the magnitude of the frequency response
From the convolution theorem, we can see that the amplitude response 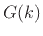 is the gain of the filter at frequency
is the gain of the filter at frequency 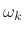 , since
, since
where
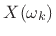 is the
is the 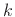 th sample of the DFT of the input signal
th sample of the DFT of the input signal
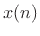 , and
, and 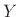 is the DFT of the output signal
is the DFT of the output signal  .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]