Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
From the above definitions, one can quickly verify
Let's verify the third relationship which states that a complex number
multiplied by its conjugate is equal to its magnitude squared:
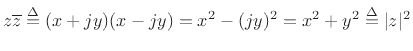 |
(2.4) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]

