Direct Proof of De Moivre's Theorem

In §2.10, De Moivre's theorem was introduced as a consequence of Euler's identity:

$$\zbox {\left[\cos(\theta) + j \sin(\theta)\right] ^n = \cos(n\theta) + j \sin(n\theta), \qquad\hbox{for all $n\in\mathbb{R}$}}$$

To provide some further insight into the ``mechanics'' of Euler's identity, we'll provide here a direct proof of De Moivre's theorem for integer $n$ using mathematical induction and elementary trigonometric identities.

Proof: To establish the ``basis'' of our mathematical induction proof, we may simply observe that De Moivre's theorem is trivially true for $n=1$ . Now assume that De Moivre's theorem is true for some positive integer $n$ . Then we must show that this implies it is also true for $n+1$ , i.e.,

$$\left[\cos(\theta) + j \sin(\theta)\right] ^{n+1} = \cos[(n+1)\theta] + j \sin[(n+1)\theta]. \protect$$ (3.2)

Since it is true by hypothesis that

$$\left[\cos(\theta) + j \sin(\theta)\right] ^n = \cos(n\theta) + j \sin(n\theta),$$

multiplying both sides by $[\cos(\theta) + j \sin(\theta)]$ yields

$$\left[\cos(\theta) + j \sin(\theta)\right] ^{n+1} = \left[\cos(n\theta) + j \sin(n\theta)\right] \cdot \left[\cos(\theta) + j \sin(\theta)\right]$$

$$= \qquad\! \left[\cos(n\theta)\cos(\theta) -\sin(n\theta)\sin(\theta)\right]$$

$$\,+\, j \left[\sin(n\theta)\cos(\theta)+\cos(n\theta)\sin(\theta)\right]. \protect$$ (3.3)

From trigonometry, we have the following sum-of-angle identities:

$$\begin{eqnarray*} \sin(\alpha+\beta) &=& \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta)\\ \cos(\alpha+\beta) &=& \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta) \end{eqnarray*}$$

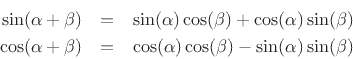
These identities can be proved using only arguments from classical geometry.^3.8Applying these to the right-hand side of Eq.(3.3), with $\alpha=n\theta$ and $\beta=\theta$ , gives Eq.(3.2), and so the induction step is proved. $\Box$

De Moivre's theorem establishes that integer powers of $[\cos(\theta) + j \sin(\theta)]$ lie on a circle of radius 1 (since $\cos^2(\phi)+\sin^2(\phi)=1$ , for all $\phi\in[-\pi,\pi]$ ). It therefore can be used to determine all $N$ of the $N$ th roots of unity (see §3.12 above). However, no definition of $e$ emerges readily from De Moivre's theorem, nor does it establish a definition for imaginary exponents (which we defined using Taylor series expansion in §3.7 above).