Rayleigh Energy Theorem (Parseval's Theorem)

Theorem: For any $x\in\mathbb{C}^N$ ,

$$\zbox {\left\Vert\,x\,\right\Vert^2 = \frac{1}{N}\left\Vert\,X\,\right\Vert^2.}$$

I.e.,

$$\zbox {\sum_{n=0}^{N-1}\left\vert x(n)\right\vert^2 = \frac{1}{N}\sum_{k=0}^{N-1}\left\vert X(k)\right\vert^2.}$$

Proof: This is a special case of the power theorem.

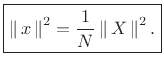
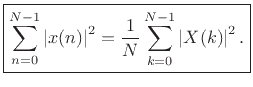
Note that again the relationship would be cleaner ( $\left\Vert\,x\,\right\Vert = \vert\vert\,\tilde{X}\,\vert\vert$ ) if we were using the normalized DFT.