Formal Statement of Taylor's Theorem

Let $f(x)$ be continuous on a real interval $I$ containing $x_0$ (and $x$ ), and let $f^{(n)}(x)$ exist at $x$ and $f^{(n+1)}(\xi)$ be continuous for all $\xi\in I$ . Then we have the following Taylor series expansion:

$$\begin{eqnarray*} f(x) = f(x_0) &+& \frac{1}{1}f^\prime(x_0)(x-x_0) \\ [10pt] &+& \frac{1}{1\cdot 2}f^{\prime\prime}(x_0)(x-x_0)^2 \\ [10pt] &+& \frac{1}{1\cdot 2\cdot 3}f^{\prime\prime\prime}(x_0)(x-x_0)^3\\ [10pt] &+& \cdots\\ [10pt] &+& \frac{1}{n!}f^{(n+1)}(x_0)(x-x_0)^n\\ [10pt] &+& R_{n+1}(x) \end{eqnarray*}$$

where $R_{n+1}(x)$ is called the remainder term. Then Taylor's theorem [66, pp. 95-96] provides that there exists some $\xi$ between $x$ and $x_0$ such that

$$R_{n+1}(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}.$$

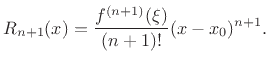
In particular, if $\vert f^{(n+1)}\vert\leq M$ in $I$ , then

$$R_{n+1}(x) \leq \frac{M \vert x-x_0\vert^{n+1}}{(n+1)!}$$

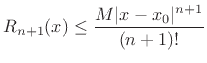
which is normally small when $x$ is close to $x_0$ .

When $x_0=0$ , the Taylor series reduces to what is called a Maclaurin series [59, p. 96].