DB SPL

Sound Pressure Level (SPL) is a dB scale defined relative to a reference that is approximately the intensity of a 1000 Hz sinusoid that is just barely audible (zero ``phons''). In pressure units, the reference root-mean-square (rms) amplitude for dB SPL calculation is^F.6

$$\begin{eqnarray*} \mbox{$0$\ dB SPL} &\isdef & \mbox{0.0002 $\mu$bar (micro-barometric pressure)} \\ &=& \mbox{20 $\mu$Pa (micro-Pascals)} \\ &=& \mbox{$2.9\times 10^{-9}$\ PSI (pounds per square inch)} \\ &=& 2\times 10^{-4}\, \frac{\mbox{\small dynes}}{\mbox{\small cm}^2} \quad\mbox{(CGS units)} \\ &=& 2\times 10^{-5}\, \frac{\mbox{\small N}}{\mbox{\small m}^2} \quad\mbox{(SI (MKS) units)}. \end{eqnarray*}$$

The dB SPL reference intensity is given by

$$I_0 = 10^{-16} \frac{\mbox{\small W}}{\mbox{\small cm}^2}.$$

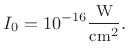
In SI units, this is $I_0 = 10^{-12}\,$   W$/$ m$^2$ .^F.7

Since sound is created by a time-varying pressure, we compute sound levels in dB-SPL by using the average fluctuation-intensity (averaged over at least one period of the lowest frequency contained in the sound).

The wave impedance of air plays the role of ``resistor'' in relating the pressure- and intensity-based references exactly analogous to the dBm case discussed above. Using a typical SI value of $R=413$ for the acoustic wave impedance (calculatable as the density of air $\rho$ times the speed of sound $c$ ), and the basic formula $I_0 = p_0^2/R$ relating intensity to rms pressure, we calculate $p_0=\sqrt{R\,I_0} = \sqrt{413\times 10^{-12}} \approx 2.03\times 10^{-5}$ , in agreement with the SI value above for the rms-pressure-reference for dB SPL.

Table F.1 gives a list of common sound levels and their dB equivalents [56]. In other references, the ``threshold of pain'' is defined as 120 dB-SPL. Note that hearing damage is a function of both level and duration of exposure.

Table F.1: Approximate dB-SPL level of common sounds. (Information from S. S. Stevens, F. Warshofsky, and the Editors of Time-Life Books, Sound and Hearing, Life Science Library, Time-Life Books, Alexandria, VA, 1965, p. 173.)

Sound	dB-SPL
Jet engine at 3m	140
Threshold of pain	130
Rock concert	120
Accelerating motorcycle at 5m	110
Pneumatic hammer at 2m	100
Noisy factory	90
Vacuum cleaner	80
Busy traffic	70
Quiet restaurant	50
Residential area at night	40
Empty movie house	30
Rustling of leaves	20
Human breathing (at 3m)	10
Threshold of hearing (good ears)	0

The relationship between sound amplitude and actual loudness is complex [79]. Loudness is a perceptual dimension while sound amplitude is physical. Since loudness sensitivity is closer to logarithmic than linear in amplitude (especially at moderate to high loudnesses), we typically use decibels to represent sound amplitude, especially in spectral displays.

The sone amplitude scale is defined in terms of actual loudness perception experiments [79]. At 1kHz and above, loudness perception is approximately logarithmic above 50 dB SPL or so. Below that, it tends toward being more linear.

The phon amplitude scale is simply the dB scale at 1kHz [79, p. 111]. At other frequencies, the amplitude in phons is defined by following the equal-loudness curve over to 1 kHz and reading off the level there in dB SPL. In other words, all pure tones have the same loudness at the same phon level, and 1 kHz is used to set the reference in dB SPL. Just remember that one phon is one dB-SPL at 1 kHz. Looking at the Fletcher-Munson equal-loudness curves [79, p. 124], loudness in phons can be read off along the vertical line at 1 kHz.

Classically, the intensity level of a sound wave is its dB SPL level, measuring the peak time-domain pressure-wave amplitude relative to $10^{-16}$ watts per centimeter squared (i.e., there is no consideration of the frequency domain here at all).

Another classical term still encountered is the sensation level of pure tones: The sensation level is the number of dB SPL above the hearing threshold at that frequency [79, p. 110].