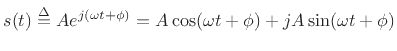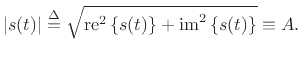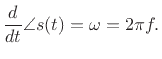Complex Sinusoids

Recall Euler's Identity,

$$e^{j\theta} = \cos(\theta) + j\sin(\theta).$$

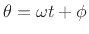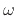Multiplying this equation by $A \geq 0$ and setting $\theta = \omega t + \phi$ , where $t$ is time in seconds, $\omega$ is radian frequency, and 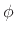$\phi$ is a phase offset, we obtain what we call the complex sinusoid:

$$s(t) \isdef A e^{j(\omega t+\phi)} = A \cos(\omega t+\phi) + jA\sin(\omega t+\phi)$$

Thus, a complex sinusoid consists of an ``in-phase'' component for its real part, and a ``phase-quadrature'' component for its imaginary part. Since $\sin^2(\theta) + \cos^2(\theta) = 1$ , we have

$$\left\vert s(t)\right\vert \isdef \sqrt{\mbox{re}^2\left\{s(t)\right\} + \mbox{im}^2\left\{s(t)\right\}} \equiv A.$$

That is, the complex sinusoid has a constant modulus (i.e., a constant complex magnitude). (The symbol ``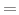$\equiv$ '' means ``identically equal to,'' i.e., for all $t$ .) The instantaneous phase of the complex sinusoid is

$$\angle s(t) = \omega t+\phi.$$

The derivative of the instantaneous phase of the complex sinusoid gives its instantaneous frequency

$$\frac{d}{dt}\angle s(t) = \omega = 2\pi f.$$