Vector Space Concepts

Definition. A set $X$ of objects is called a metric space if with any two points $p$ and $q$ of $X$ there is associated a real number $d(p,q)$, called the distance from $p$ to $q$, such that (a) $d(p,q)>0$ if $p\neq q$; $d(p,p)=0$, (b) $d(p,q)=d(q,p)$, (c) $d(p,q)\leq d(p,r)+d(r,q)$, for any $r\in X$ [6].

Definition. A linear space is a set of ``vectors'' $X$ together with a field of ``scalars'' ${\cal S}$ with an addition operation $+:X\times X\mapsto X$, and a multiplication opration $\cdot$ taking ${\cal S}\times X\mapsto X$, with the following properties: If $x$, $y$, and $z$ are in $X$, and $\alpha,\beta$ are in ${\cal S}$, then

1. $x+y=y+x$.
2. $x+(y+z)=(x+y)+z$.
3. There exists $\emptyset$ in $X$ such that $0\cdot x=\emptyset$ for all $x$ in $X$.
4. $\alpha(\beta x) = (\alpha\beta) x$.
5. $(\alpha+\beta)x=\alpha x + \beta x$.
6. $1\cdot x = x$.
7. $\alpha(x+y) = \alpha x + \alpha y$.

The element $\emptyset$ is written as 0 thus coinciding with the notation for the real number zero. A linear space is sometimes be called a linear vector space, or a vector space.

Definition. A normed linear space is a linear space $X$ on which there is defined a real-valued function of $x\in X$ called a norm, denoted $\vert\vert\,x\,\vert\vert$, satisfying the following three properties:

1. $\left\Vert\,x\,\right\Vert \geq 0$, and $\left\Vert\,x\,\right\Vert=0 \Leftrightarrow x=0$.
2. $\left\Vert\,cx\,\right\Vert = \left\vert c\right\vert\cdot\left\Vert\,x\,\right\Vert$, $c$ a scalar.
3. $\left\Vert\,x_1+x_2\,\right\Vert \leq \left\Vert\,x_1\,\right\Vert + \left\Vert\,x_2\,\right\Vert$.

The functional $\vert\vert\,x-y\,\vert\vert$ serves as a distance function on $X$, so a normed linear space is also a metric space.

Note that when $X$ is the space of continuous complex functions on the unit circle in the complex plane, the norm of a function is not changed when multiplied by a function of modulus $1$ on the unit circle. In signal processing terms, the norm is insensitive to multiplication by a unity-gain allpass filter (also known as a Blaschke product).

Definition. A pseudo-norm is a real-valued function of $x\in X$ satisfying the following three properties:

1. $\left\Vert\,x\,\right\Vert \geq 0$, and $x=0\implies\left\Vert\,x\,\right\Vert=0$.
2. $\left\Vert\,cx\,\right\Vert = \left\vert c\right\vert\cdot\left\Vert\,x\,\right\Vert$, $c$ a scalar.
3. $\left\Vert\,x_1+x_2\,\right\Vert \leq \left\Vert\,x_1\,\right\Vert + \left\Vert\,x_2\,\right\Vert$.

A pseudo-norm differs from a norm in that the pseudo-norm can be zero for nonzero vectors (functions).

Definition. A Banach Space is a complete normed linear space, that is, a normed linear space in which every Cauchy sequence¹converges to an element of the space.

Definition. A function $H(e^{j\omega})$ is said to belong to the space $Lp$ if

$$\int_{-\pi}^\pi \left\vert H(e^{j\omega})\right\vert^p{d\omega\over 2\pi}< \infty.$$

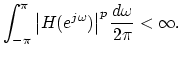
Definition. A function $H(e^{j\omega})$ is said to belong to the space $H^p$ if it is in $Lp$ and if its analytic continuation $H(z)$ is analytic for $\vert z\vert<1$. $H(z)$ is said to be in $H^{-p}$ if $H(z^{-1})\in H^p$.

Theorem. (Riesz-Fischer) The $Lp$ spaces are complete. Proof. See Royden [5], p. 117.

Definition. A Hilbert space is a Banach space with a symmetric bilinear inner product $<x,y>$ defined such that the inner product of a vector with itself is the square of its norm $<x,x>= \vert\vert\,x\,\vert\vert ^2$.