Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The transfer function of an FIR filter is given by the z transform of
its impulse response. This is true for any LTI filter, as discussed
in Chapter 6. For FIR filters in particular, we have, from
Eq.(5.6),
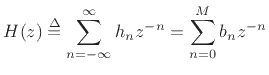 |
(6.8) |
Thus, the transfer function of every length 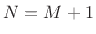 FIR filter
is an
FIR filter
is an 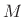 th-order polynomial in
th-order polynomial in 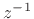 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]