We will now derive the convolution representation for causal LTI filters
in its full generality. The first step is to express an arbitrary signal
![]() as a linear combination of shifted impulses, i.e.,
as a linear combination of shifted impulses, i.e.,
If the above equation is not obvious, here is how it is built up
intuitively. Imagine
![]() as a 1 in the midst of an
infinite string of 0s. Now think of
as a 1 in the midst of an
infinite string of 0s. Now think of
![]() as the same
pattern shifted over to the right by
as the same
pattern shifted over to the right by ![]() samples. Next multiply
samples. Next multiply
![]() by
by ![]() , which plucks out the sample
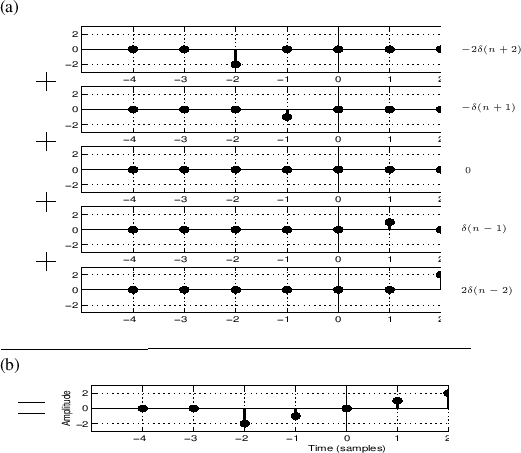
, which plucks out the sample ![]() and surrounds it on both sides by 0's. An example collection of
waveforms
and surrounds it on both sides by 0's. An example collection of
waveforms
![]() for the case
for the case
![]() is shown in
Fig.5.4a. Now, sum over all
is shown in
Fig.5.4a. Now, sum over all ![]() , bringing together the
samples of
, bringing together the
samples of ![]() , to obtain
, to obtain ![]() . Figure 5.4b
shows the result of this addition for the sequences in
Fig.5.4a. Thus, any signal
. Figure 5.4b
shows the result of this addition for the sequences in
Fig.5.4a. Thus, any signal ![]() may be expressed as a
weighted sum of shifted impulses.
may be expressed as a
weighted sum of shifted impulses.
Equation (5.4) expresses a signal as a linear combination (or weighted sum) of impulses. That is, each sample may be viewed as an impulse at some amplitude and time. As we have already seen, each impulse (sample) arriving at the filter's input will cause the filter to produce an impulse response. If another impulse arrives at the filter's input before the first impulse response has died away, then the impulse response for both impulses will superimpose (add together sample by sample). More generally, since the input is a linear combination of impulses, the output is the same linear combination of impulse responses. This is a direct consequence of the superposition principle which holds for any LTI filter.
 |
We repeat this in more precise terms. First linearity is used and then time-invariance is invoked. Using the form of the general linear filter in Eq.(4.2), and the definition of linearity, Eq.(4.3) and Eq.(4.5), we can express the output of any linear (and possibly time-varying) filter by
where we have written
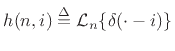 to denote the filter
response at time
to denote the filter
response at time ![]() to an impulse which occurred at time
to an impulse which occurred at time ![]() . If we are
to be completely rigorous mathematically, certain ``smoothness''
restrictions must be placed on the linear operator
. If we are
to be completely rigorous mathematically, certain ``smoothness''
restrictions must be placed on the linear operator ![]() in order that
it may be distributed inside the infinite summation [37].
However, practically useful filters of the
form of Eq.(5.1) satisfy these restrictions. If in addition to
being linear, the filter is time-invariant, then
in order that
it may be distributed inside the infinite summation [37].
However, practically useful filters of the
form of Eq.(5.1) satisfy these restrictions. If in addition to
being linear, the filter is time-invariant, then
![]() ,
which allows us to write
,
which allows us to write
The infinite sum
in Eq.(5.5) can be replaced by more typical practical
limits. By choosing time 0 as the beginning of the signal, we may
define ![]() to be 0 for
to be 0 for ![]() so that the lower summation limit of
so that the lower summation limit of
![]() can be replaced by 0. Also, if the filter is causal, we
have
can be replaced by 0. Also, if the filter is causal, we
have ![]() for
for ![]() , so the upper summation limit can be
written as
, so the upper summation limit can be
written as ![]() instead of
instead of ![]() . Thus, the
convolution representation of a linear, time-invariant, causal
digital filter is given by
. Thus, the
convolution representation of a linear, time-invariant, causal
digital filter is given by
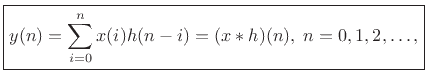
for causal input signals (i.e.,
Since the above equation is a convolution, and since convolution is
commutative (i.e.,
![]() [84]), we
can rewrite it as
[84]), we
can rewrite it as
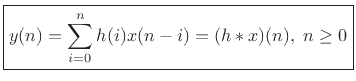
or
This latter form looks more like the general difference equation presented in Eq.(5.1). In this form one can see that