The general second-order case with ![]() (the so-called
biquad section) can be written when
(the so-called
biquad section) can be written when ![]() as
as
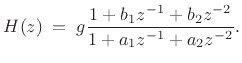
To perform a partial fraction expansion, we need to extract an order 0 (length 1) FIR part via long division. Let
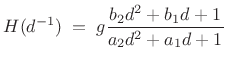
Then long division gives
![% For typesetting long division --- NEEDED WITHIN THE MAKEIMAGE ENV?
% (raw TeX, not LaTeX)\begin{displaymath}
\begin{array}[t]{@{}rcccc@{}}
& & & \frac{b_2}{a_2} & \\ [5pt] %
\noalign{\moveright 9.5\digitwidth%
\vbox{\hrule width 22\digitwidth}}
a_2~~a_1~~1~\bigg)\,
& b_2 & b_1 & 1 & \\
& b_2 & \frac{b_2}{a_2}a_1 & \frac{b_2}{a_2} &\\ [5pt] %
\noalign{\moveright 11\digitwidth%
\vbox{\hrule width 22\digitwidth}}\vspace{5pt}
& & b_1-\frac{b_2}{a_2}a_1 & 1-\frac{b_2}{a_2} &
\end{array}\end{displaymath}](img741.png)
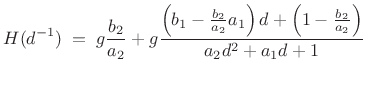
or
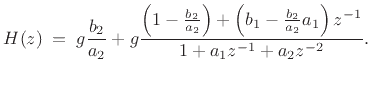
The delayed form of the partial fraction expansion is obtained by
leaving the coefficients in their original order. This corresponds
to writing ![]() as a ratio of polynomials in
as a ratio of polynomials in ![]() :
:
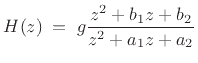
Long division now looks like
![% For typesetting long division --- NEEDED WITHIN THE MAKEIMAGE ENV?\begin{displaymath}
\begin{array}[t]{@{}rcccc@{}}
& & & 1 & \\ %
\noalign{\moveright 9.5\digitwidth%
\vbox{\hrule width 22\digitwidth}}
1~~a_1~~a_2~\bigg)\,
& ~1~~ &b_1 & b_2 & \\
& ~1~~ & a_1 & a_2 &\\ %
\noalign{\moveright 11\digitwidth%
\vbox{\hrule width 22\digitwidth}}
& & b_1-a_1 & b_2-a_2 &
\end{array}\end{displaymath}](img745.png)
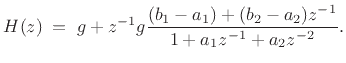
Numerical examples of partial fraction expansions are given in §6.8.8
below. Another worked example, in which the filter
![]() is converted to a set of parallel, second-order
sections is given in §3.12. See also §9.2 regarding
conversion to second-order sections in general, and §G.9.1 (especially
Eq.(G.22)) regarding
a state-space approach to partial fraction expansion.
is converted to a set of parallel, second-order
sections is given in §3.12. See also §9.2 regarding
conversion to second-order sections in general, and §G.9.1 (especially
Eq.(G.22)) regarding
a state-space approach to partial fraction expansion.