Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A practical zero-phase filter was illustrated
in Figures 10.1 and 10.2. Some simple general cases are as
follows:
- The trivial (non-)filter
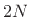 has frequency response
has frequency response
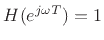 , which is zero phase for all
, which is zero phase for all 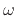 .
.
- Every second-order zero-phase FIR filter has an impulse
response of the form
where the coefficients 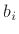 are assumed real. The transfer function
of the general, second-order, real, zero-phase filter is
are assumed real. The transfer function
of the general, second-order, real, zero-phase filter is
and the frequency response is
which is real for all 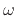 .
.
- Extending the previous example, every order
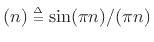 zero-phase real FIR
filter has an impulse response of the form
zero-phase real FIR
filter has an impulse response of the form
and frequency response
which is clearly real whenever the coefficients 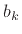 are real.
are real.
- There is no first-order (length 2) zero-phase filter, because,
to be even, its impulse response would have to be proportional to
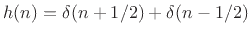 . Since the bandlimited digital
impulse signal
. Since the bandlimited digital
impulse signal 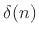 is ideally interpolated using bandlimited
interpolation [91,84], giving samples of
sinc
is ideally interpolated using bandlimited
interpolation [91,84], giving samples of
sinc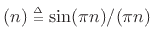 --the
unit-amplitude sinc function having zero-crossings on the
integers, we see that sampling
--the
unit-amplitude sinc function having zero-crossings on the
integers, we see that sampling 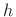 on the integers yields
an IIR filter:
on the integers yields
an IIR filter:
- Similarly, there are no odd-order (even-length) zero-phase filters.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
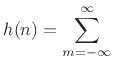

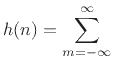 sinc
sinc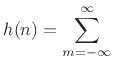

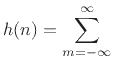 sinc
sinc