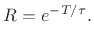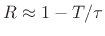Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A useful approximate formula giving the decay
time-constant9.4  (in
seconds) in terms of a pole radius
(in
seconds) in terms of a pole radius 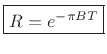 is
is
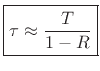 |
(9.8) |
where 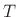 denotes the sampling interval in seconds, and we assume
denotes the sampling interval in seconds, and we assume 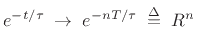 .
.
The exact relation between  and
and 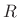 is obtained by sampling an
exponential decay:
is obtained by sampling an
exponential decay:
Thus, setting 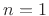 yields
yields
Expanding the right-hand side in a Taylor series and neglecting terms
higher than first order gives
which derives
 . Solving for
. Solving for  then gives
Eq.(8.8). From its derivation, we see that the approximation is
valid for
then gives
Eq.(8.8). From its derivation, we see that the approximation is
valid for 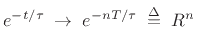 . Thus, as long as the impulse response of a pole
. Thus, as long as the impulse response of a pole
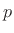 ``rings'' for many samples, the formula
``rings'' for many samples, the formula
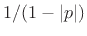 should well estimate the time-constant of decay in seconds. The
time-constant estimate in samples is of course
should well estimate the time-constant of decay in seconds. The
time-constant estimate in samples is of course 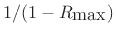 . For
higher-order systems, the approximate decay time is
. For
higher-order systems, the approximate decay time is
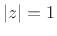 , where
, where
 is the largest pole
magnitude (closest to the unit circle) in the (stable) system.
is the largest pole
magnitude (closest to the unit circle) in the (stable) system.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() (in
seconds) in terms of a pole radius
(in
seconds) in terms of a pole radius ![]() is
is
![]() and
and ![]() is obtained by sampling an
exponential decay:
is obtained by sampling an
exponential decay: