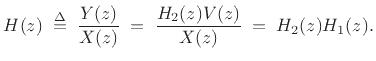Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure 6.1 illustrates the series connection of two
filters
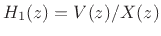 and
and
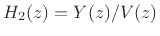 .
The output
.
The output 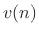 from filter 1 is used as the input to filter 2.
Therefore, the overall transfer function is
from filter 1 is used as the input to filter 2.
Therefore, the overall transfer function is
In summary, if the output of filter 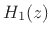 is given as input to
filter
is given as input to
filter  (a series combination), as shown in Fig.6.1, the
overall transfer function is
(a series combination), as shown in Fig.6.1, the
overall transfer function is
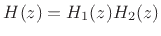 --transfer
functions of filters connected in series multiply together.
--transfer
functions of filters connected in series multiply together.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
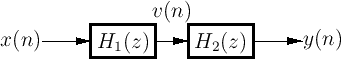
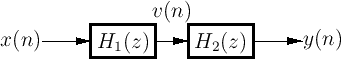
![]() and
and
![]() .
The output
.
The output ![]() from filter 1 is used as the input to filter 2.
Therefore, the overall transfer function is
from filter 1 is used as the input to filter 2.
Therefore, the overall transfer function is