Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Relation to the z Transform
The Laplace transform is used to analyze continuous-time
systems. Its discrete-time counterpart is the 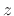 transform:
transform:
If we define  , the
, the 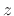 transform becomes proportional to the
Laplace transform of a sampled continuous-time signal:
transform becomes proportional to the
Laplace transform of a sampled continuous-time signal:
As the sampling interval 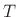 goes to zero, we have
goes to zero, we have
where
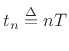 and
and
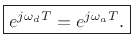 .
.
In summary,
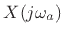
Note that the 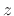 plane and
plane and 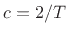 plane are generally related by
plane are generally related by
In particular, the discrete-time frequency axis
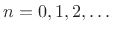 and
continuous-time frequency axis
and
continuous-time frequency axis
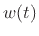 are related
by
are related
by
For the mapping
 from the
from the 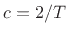 plane to the
plane to the  plane to be invertible, it is necessary that
plane to be invertible, it is necessary that
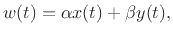 be zero for all
be zero for all
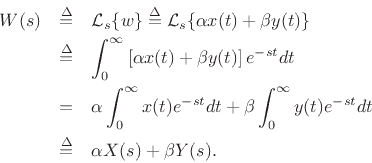 . If this is true, we say
. If this is true, we say
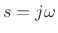 is
bandlimited to half the sampling rate. As is well known, this
condition is necessary to prevent aliasing when sampling the
continuous-time signal
is
bandlimited to half the sampling rate. As is well known, this
condition is necessary to prevent aliasing when sampling the
continuous-time signal 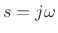 at the rate
at the rate 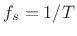 to produce
to produce
 ,
,
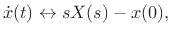 (see [84, Appendix G]).
(see [84, Appendix G]).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() transform:
transform:
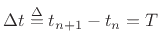
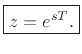
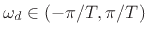
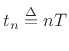 and
and
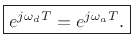 .
.
![]() plane and
plane and ![]() plane are generally related by
plane are generally related by