Let's repeat the mathematical sine-wave analysis of the simplest
low-pass filter, but this time using a complex sinusoid instead of a
real one. Thus, we will test the filter's response at frequency ![]() by setting its input to
by setting its input to
Again, because of time-invariance, the frequency response will not depend on
Using the normal rules for manipulating exponents, we find that the
output of the simple low-pass filter in response to the complex
sinusoid at frequency
![]() Hz is given by
Hz is given by
 , which we
will show is in fact the frequency response of this filter at
frequency
, which we
will show is in fact the frequency response of this filter at
frequency
where the gain versus frequency is given by
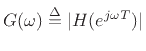 (the absolute value, or modulus of
(the absolute value, or modulus of
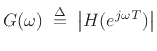
which is the amplitude response, and
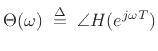
which is the phase response. There is a trick we can call ``balancing the exponents,'' which will work nicely for the simple low-pass of Eq.(1.1).
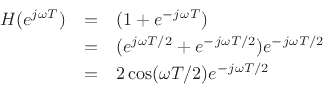
It is now easy to see that
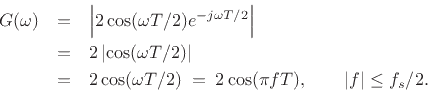
and
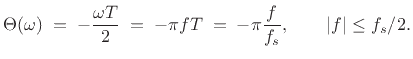
We have derived again the graph of Fig.1.7, which shows the complete frequency response of Eq.(1.1). The gain of the simplest low-pass filter varies, as cosine varies, from 2 to 0 as the frequency of an input sinusoid goes from 0 to half the sampling rate. In other words, the amplitude response of Eq.(1.1) goes sinusoidally from 2 to 0 as
It deserves to be emphasized that all a linear time-invariant filter
can do to a sinusoid is scale its amplitude and change
its phase. Since a sinusoid is completely determined by its amplitude
![]() , frequency
, frequency ![]() , and phase
, and phase ![]() , the constraint on the filter is
that the output must also be a sinusoid, and furthermore it must be at
the same frequency as the input sinusoid. More explicitly:
, the constraint on the filter is
that the output must also be a sinusoid, and furthermore it must be at
the same frequency as the input sinusoid. More explicitly:
Mathematically, a sinusoid has no beginning and no end, so there really are no start-up transients in the theoretical setting. However, in practice, we must approximate eternal sinusoids with finite-time sinusoids whose starting time was so long ago that the filter output is essentially the same as if the input had been applied forever.
Tying it all together, the general output of a linear time-invariant filter with a complex sinusoidal input may be expressed as
![\begin{eqnarray*}
y(n) &=& (\textit{Complex Filter Gain}) \;\textit{times}\;\, (\textit{Input Circular Motion}\\
& & \textit{with Radius $A$, Phase $\phi$})\\
&=& \left[ G(\omega) e^{j\Theta(\omega)}\right]
\left[ A e^{j(\omega n T + \phi)}\right]\\
&=& \left[ G(\omega) A\right] e^{j[\omega n T + \phi+\Theta(\omega)]}\\
&=& \textit{Circular Motion with Radius $[G(\omega)A]$\ and Phase $[\phi + \Theta(\omega)]$}.
\end{eqnarray*}](img242.png)