Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We derived the frequency response above using trig identities in order
to minimize the mathematical level involved. However, it turns out it
is actually easier, though more advanced, to use complex
numbers for this purpose. To do this, we need Euler's
identity:
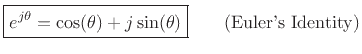 |
(2.8) |
where
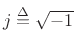 is the imaginary unit for complex numbers,
and
is the imaginary unit for complex numbers,
and 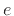 is a transcendental constant approximately equal to
is a transcendental constant approximately equal to
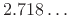 . Euler's identity is fully derived in
[84]; here we will simply use it ``on faith.'' It can be
proved by computing the Taylor series expansion of each side of
Eq.(1.8) and showing equality term by term [84,14].
. Euler's identity is fully derived in
[84]; here we will simply use it ``on faith.'' It can be
proved by computing the Taylor series expansion of each side of
Eq.(1.8) and showing equality term by term [84,14].
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
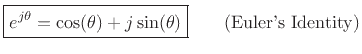
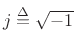 is the imaginary unit for complex numbers,
and
is the imaginary unit for complex numbers,
and