Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In the simple RC-filter example of §E.4.3, the transfer function is
Thus, there is a single pole at
 , and we can say
there is one zero at infinity as well. Since resistors and
capacitors always have positive values, the time constant
, and we can say
there is one zero at infinity as well. Since resistors and
capacitors always have positive values, the time constant 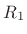 is always non-negative. This means the impulse response is always an
exponential decay--never a growth. Since the pole is at
is always non-negative. This means the impulse response is always an
exponential decay--never a growth. Since the pole is at
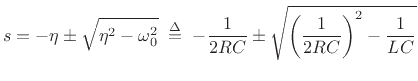 , we find that it is always in the left-half
, we find that it is always in the left-half 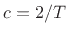 plane. This turns out to be the case also for any complex
analog one-pole filter. By consideration of the partial fraction
expansion of any
plane. This turns out to be the case also for any complex
analog one-pole filter. By consideration of the partial fraction
expansion of any 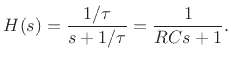 , it is clear that, for stability of an analog
filter, all poles must lie in the left half of the complex
, it is clear that, for stability of an analog
filter, all poles must lie in the left half of the complex 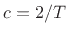 plane. This is the analog counterpart of the requirement for digital
filters that all poles lie inside the unit circle.
plane. This is the analog counterpart of the requirement for digital
filters that all poles lie inside the unit circle.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]

