In this section, we show that the poles of a state-space model are given
by the eigenvalues of the state-transition matrix ![]() .
.
Beginning again with the transfer function of the general state-space model,
we may first observe that the poles of
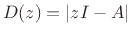
(They are the same when all modes are controllable and observable [37].) By Cramer's rule for matrix inversion, the denominator polynomial for
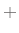
where
Thus, the eigenvalues of the state transition matrix ![]() are the
poles of the corresponding linear time-invariant system. In
particular, note that the poles of the system do not depend on the
matrices
are the
poles of the corresponding linear time-invariant system. In
particular, note that the poles of the system do not depend on the
matrices ![]() , although these matrices, by placing system zeros,
can cause pole-zero cancellations (unobservable or uncontrollable
modes).
, although these matrices, by placing system zeros,
can cause pole-zero cancellations (unobservable or uncontrollable
modes).