Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
From Eq.(6.5), we have
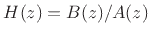 , so that the
frequency response is
, so that the
frequency response is
and
where
and the DTFT is as defined in Eq.(7.1).
From the above relations, we may express the frequency response of any
IIR filter as a ratio of two finite DTFTs:
 |
(8.5) |
This expression provides a convenient basis for the computation of an
IIR frequency response in software, as we pursue further in the next
section.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , so that the
frequency response is
, so that the
frequency response is
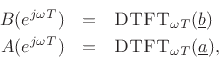
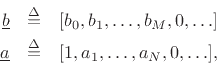
![\begin{eqnarray*}
{\underline{b}}&\isdef & [b_0,b_1,\ldots,b_M,0,\ldots]\\
{\underline{a}}&\isdef & [1,a_1,\ldots,a_N,0,\ldots],
\end{eqnarray*}](img855.png)