The differentiation theorem for Laplace transforms states that
where
 , and
, and
Proof:
This follows immediately from integration by parts:
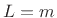
since
![]() by assumption.
by assumption.
Corollary: Integration Theorem
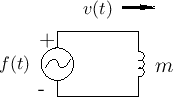
Thus, successive time derivatives correspond to successively higher
powers of ![]() , and successive integrals with respect to time
correspond to successively higher powers of
, and successive integrals with respect to time
correspond to successively higher powers of ![]() .
.