Suppose we write a narrowband signal centered at frequency ![]() as
as
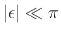
for some
Using the above frequency-domain expansion of ![]() ,
, ![]() can be
written as
can be
written as
![$\displaystyle x(n) \eqsp a_m(n) e^{j\omega_c n} \eqsp
\left[\frac{1}{2\pi} \int_{-\epsilon}^{\epsilon} A_m(\omega)e^{j\omega n} d\omega\right] e^{j\omega_c n},
$](img908.png)
which we may view as a scaled superposition of sinusoidal components of the form
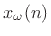
with
to get
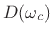
where
![\begin{eqnarray*}
y_\omega(n)
&=& \left[G(\omega_c+\omega)A_m(\omega)\right]
e^{j[(\omega_c +\omega) n + \Theta(\omega_c) - D(\omega_c)\omega]}\\
&=& \left[G(\omega_c+\omega)A_m(\omega)\right]
e^{j\{[\omega_c n + \Theta(\omega_c)] +\omega[n - D(\omega_c)]\}}\\
&=& \left[G(\omega_c+\omega)A_m(\omega)\right]
e^{j\omega[n-D(\omega_c)]} e^{j\omega_c[n-P(\omega_c)]},
\end{eqnarray*}](img916.png)
where we also used the definition of phase delay,
![]() , in the last step. In this expression we
can already see that the carrier sinusoid is delayed by the phase
delay, while the amplitude-envelope frequency-component is delayed by
the group delay. Integrating over
, in the last step. In this expression we
can already see that the carrier sinusoid is delayed by the phase
delay, while the amplitude-envelope frequency-component is delayed by
the group delay. Integrating over ![]() to recombine the
sinusoidal components (i.e., using a Fourier superposition integral for
to recombine the
sinusoidal components (i.e., using a Fourier superposition integral for
![]() ) gives
) gives
![\begin{eqnarray*}
y(n) &=& \frac{1}{2\pi}\int_{\omega} y_\omega(n) d\omega \\
&=&
\left\{\frac{1}{2\pi}\int_{-\pi}^{\pi}
\left[G(\omega_c+\omega)A_m(\omega)\right]
e^{j\omega[n-D(\omega_c)]} d\omega\right\}
e^{j\omega_c[n-P(\omega_c)]}\\
&=& a^f[n-D(\omega_c)] \cdot e^{j\omega_c[n-P(\omega_c)]}
\end{eqnarray*}](img918.png)
where ![]() denotes a zero-phase filtering of the amplitude
envelope
denotes a zero-phase filtering of the amplitude
envelope ![]() by
by
![]() . We see that the amplitude
modulation is delayed by
. We see that the amplitude
modulation is delayed by
![]() while the carrier wave is
delayed by
while the carrier wave is
delayed by
![]() .
.
We have shown that, for narrowband signals expressed as in Eq.(7.6) as a modulation envelope times a sinusoidal carrier, the carrier wave is delayed by the filter phase delay, while the modulation is delayed by the filter group delay, provided that the filter phase response is approximately linear over the narrowband frequency interval.