Capacitors

A capacitor can be made physically using two parallel conducting plates which are held close together (but not touching). Electric charge can be stored in a capacitor by applying a voltage across the plates.

The defining equation of a capacitor $C$ is

$$q(t) = Cv(t) \protect$$ (E.2)

where $q(t)$ denotes the capacitor's charge in Coulombs, $C$ is the capacitance in Farads, and $v(t)$ is the voltage drop across the capacitor in volts. Differentiating with respect to time gives

$$i(t) = C\frac{dv(t)}{dt},$$

where $i(t)\isdef dq(t)/dt$ is now the current in Amperes. Note that, by convention, the current is taken to be positive when flowing from plus to minus across the capacitor (see the arrow in Fig.E.1 which indicates the direction of current flow--there is only one current $i(t)$ flowing clockwise around the loop formed by the voltage source, resistor, and capacitor when an external voltage $v_e$ is applied).

Taking the Laplace transform of both sides gives

$$I(s) = Cs V(s) - Cv(0),$$

by the differentiation theorem for Laplace transforms (§D.4.2).

Assuming a zero initial voltage across the capacitor at time 0, we have

$$R_C(s) \isdef \frac{V(s)}{I(s)} = \frac{1}{Cs}.$$

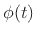
We call this the driving-point impedance of the capacitor. The driving-point impedance facilitates steady state analysis (zero initial conditions) by allowing the capacitor to be analyzed like a simple resistor, with value $1/(Cs)$ Ohms.