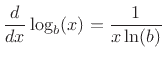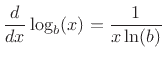Exercises

1. Show that
   $$\frac{d}{dx}\log_b(x) = \frac{1}{x\ln(b)}$$
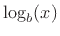   where $\log_b(x)$ denotes the logarithm to the base 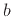$b$ of $x$ .

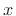2. Work out the definition of logarithms using a complex base $b$ .

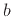3. Try synthesizing a sawtooth waveform which increases by 1/2 dB a few times per second, and again using 1/4 dB increments. See if you agree that quarter-dB increments are ``smooth'' enough for you.