Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Implemented Model for Masking Threshold
To produce the masking threshold from the spread function and the masker,
we need to know the tonality 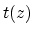 and the spreading function
and the spreading function
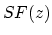 of the masker.
After an idea taken
MPEG-1 layer I [2], the following model for masking threshold
of the masker.
After an idea taken
MPEG-1 layer I [2], the following model for masking threshold
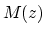 is used:
is used:
 |
(14) |
where 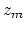 is the frequency in barks for the masker,
is the frequency in barks for the masker, 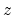 is the masked
frequency in barks and
is the masked
frequency in barks and 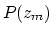 is the power of the masker in dB.
The functions
is the power of the masker in dB.
The functions 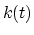 and
and 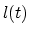 are experimentally found as a linear
combinations of constants for pure noise and pure tones:
are experimentally found as a linear
combinations of constants for pure noise and pure tones:
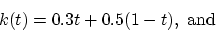 |
(15) |
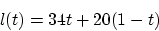 |
(16) |
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bosse.pdf
![]() and the spreading function
and the spreading function
![]() of the masker.
After an idea taken
MPEG-1 layer I [2], the following model for masking threshold
of the masker.
After an idea taken
MPEG-1 layer I [2], the following model for masking threshold
![]() is used:
is used: