Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The tonality of a frequency bin
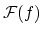 is estimated by looking
at the predictability of the phase and magnitude of that
Fourier coefficient. The predictors are defined as follows:
is estimated by looking
at the predictability of the phase and magnitude of that
Fourier coefficient. The predictors are defined as follows:
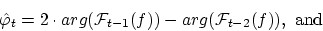 |
(11) |
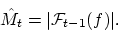 |
(12) |
The phase is thus linearly extrapolated from two former time instances, and
magnitude is simply assumed to be the same as last. This gives no
prediction error for one stationary sine within the frequency band.
The tonality is then estimated from the maximum prediction error of the
last two phase values and the last magnitude:
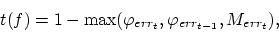 |
(13) |
where
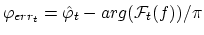 and
and
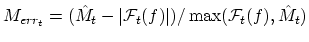 . This model gives
a weighted average
. This model gives
a weighted average 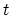 of about 0.9 for highly tonal sting music,
and 0.3 for white
noise. Of course the parameters in the masking threshold (section
3.2.5) estimation is
adapted to these (non-ideal) values.
of about 0.9 for highly tonal sting music,
and 0.3 for white
noise. Of course the parameters in the masking threshold (section
3.2.5) estimation is
adapted to these (non-ideal) values.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bosse.pdf