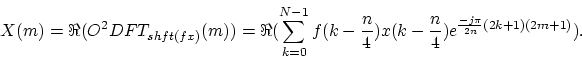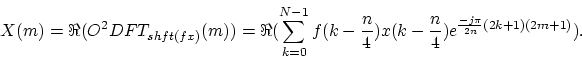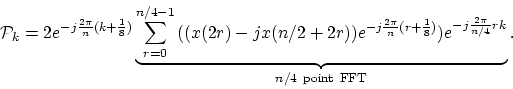Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The MDCT can be calculated using FFT. The naive approach, though, requires
a 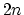 length FFT for a length
length FFT for a length 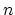 block, because of the odd
transform. There are faster approaches though [6]. The MDCT can
be rewritten as an odd-time odd-frequency discrete Fourier transform
(O
block, because of the odd
transform. There are faster approaches though [6]. The MDCT can
be rewritten as an odd-time odd-frequency discrete Fourier transform
(O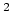 DFT)
DFT)
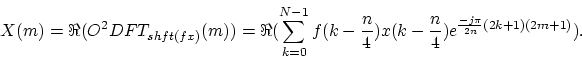 |
(23) |
[6] presents a fast algorithm for calculating
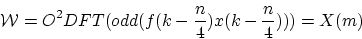 |
(24) |
as
where
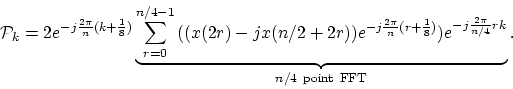 |
(28) |
Thus, the MDCT can be calculated using only one  point FFT and some
pre- and post-rotation of the sample points. The IMDCT can be calculated in
a similar way. See the code for a more detailed description.
point FFT and some
pre- and post-rotation of the sample points. The IMDCT can be calculated in
a similar way. See the code for a more detailed description.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bosse.pdf