Karhunen Lòeve Transform (KLT)

The KLT is a linear transform where the basis functions are taken from the statistics of the signal, and can thus be adaptive. It is optimal in the sense of energy compaction, i.e it places as much energy as possible in as few coefficients as possible. The KLT is also called Principal Component Analysis, and for discrete signals, the is also equivalent with the Singular Value Decomposition. The transform is generally not separable, and thus the full matrix multiplication must be performed:

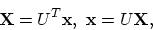$${\bf X} = U^T{\bf x},\ {\bf x} = U{\bf X},$$ (29)

where the 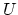$U$ is the basis for the transform. 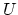$U$ is estimated from a number of ${\bf x}_i,\ i\in [0..k]$:

$$U\Sigma V^T = [{\bf x}_1\ {\bf x}_2\ \ldots\ {\bf x}_k] = A \Rightarrow U = {\rm eigvec}(AA^T)$$ (30)

The adaptiveness is not used in the coder, and the basis functions are calculated off-line in MatLab.