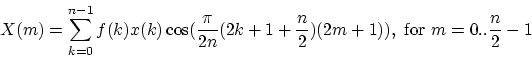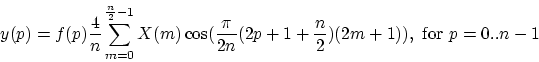Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Modified Discrete Cosine Transform (MDCT)
The MDCT is a linear orthogonal lapped transform, based on the idea of time
domain aliasing cancellation (TDAC). It was first introduced in
[3], and further developed in [4].
MDCT is critically sampled, which means that though it is 50% overlapped,
a sequence data represented with MDCT coefficients takes equally much
space as the original data.
This means, that a single block of IMDCT data does not correspond
to the original block, on which the MDCT was performed, but rather to the
odd part of that. When subsequent blocks of inverse transformed
data are added (still using 50% overlap), the errors introduced by the
transform cancels out  TDAC. Thanks to the overlapping
feature, the MDCT is very useful for quantization. It effectively removes the
otherwise easily detectable blocking artifact between transform blocks.
The used definition of MDCT is (a slight modification from [5]) is:
TDAC. Thanks to the overlapping
feature, the MDCT is very useful for quantization. It effectively removes the
otherwise easily detectable blocking artifact between transform blocks.
The used definition of MDCT is (a slight modification from [5]) is:
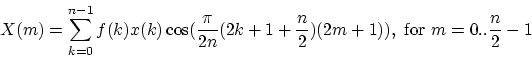 |
(20) |
and the IMDCT:
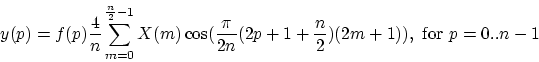 |
(21) |
where 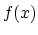 is a window with certain properties (see [5]). The
sine window
is a window with certain properties (see [5]). The
sine window
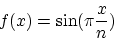 |
(22) |
has the right properties, and is used in this coder. The MDCT in the coder
is performed
with a length of 512, and thus 256 new samples are used for every block.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bosse.pdf
![]() TDAC. Thanks to the overlapping
feature, the MDCT is very useful for quantization. It effectively removes the
otherwise easily detectable blocking artifact between transform blocks.
The used definition of MDCT is (a slight modification from [5]) is:
TDAC. Thanks to the overlapping
feature, the MDCT is very useful for quantization. It effectively removes the
otherwise easily detectable blocking artifact between transform blocks.
The used definition of MDCT is (a slight modification from [5]) is: