The Rectangular Window

Previously, we looked at the rectangular window:

$$w_R(n) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left\{\begin{array}{ll} 1, & \left\vert n\right\vert\leq\frac{M-1}{2} \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right.$$

The window transform (DTFT) was found to be

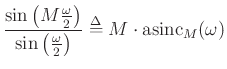$$W_R(\omega) = \frac{\sin\left(M\frac{\omega}{2}\right)}{\sin\left(\frac{\omega}{2}\right)} \mathrel{\stackrel{\mathrm{\Delta}}{=}}M\cdot \hbox{asinc}_M(\omega)$$ (1)

where $\hbox{asinc}_M(\omega)$ denotes the aliased sinc function.

$$\hbox{asinc}_M(\omega) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\frac{\sin(M\omega/2)}{M\cdot \sin(\omega/2)}$$

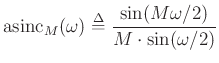
This result is plotted below:

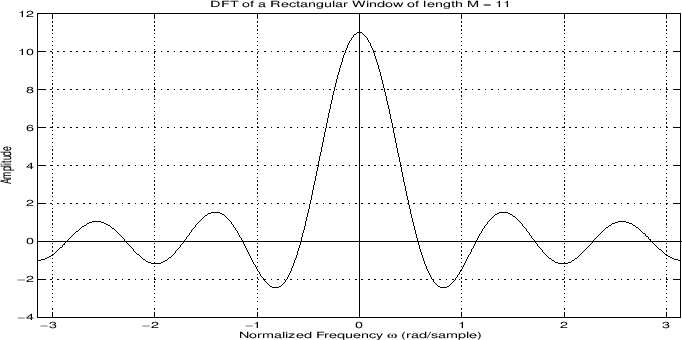
Note that this is the complete window transform, not just its magnitude. We obtain real window transforms like this only for symmetric, zero-centered windows.

More generally, we may plot both the magnitude and phase of the window versus frequency:

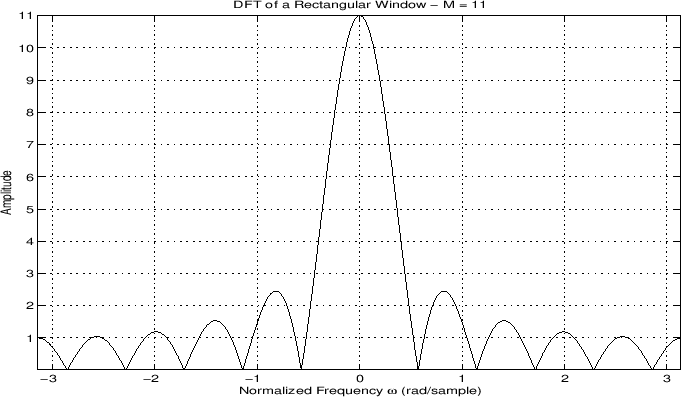
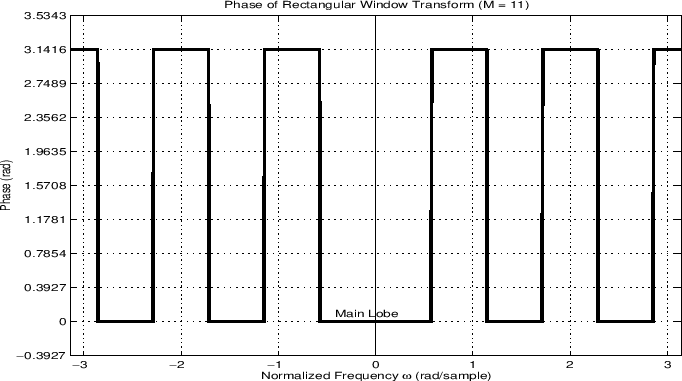
In audio work, we more typically plot the window transform magnitude on a decibel (dB) scale:

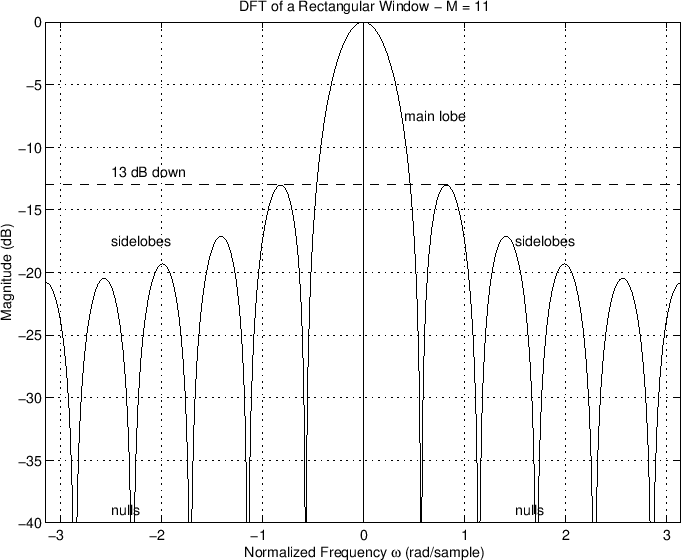
Since the DTFT of the rectangular window approximates the sinc function, it should ``roll off'' at approximately 6 dB per octave, as verified in the log-log plot below:

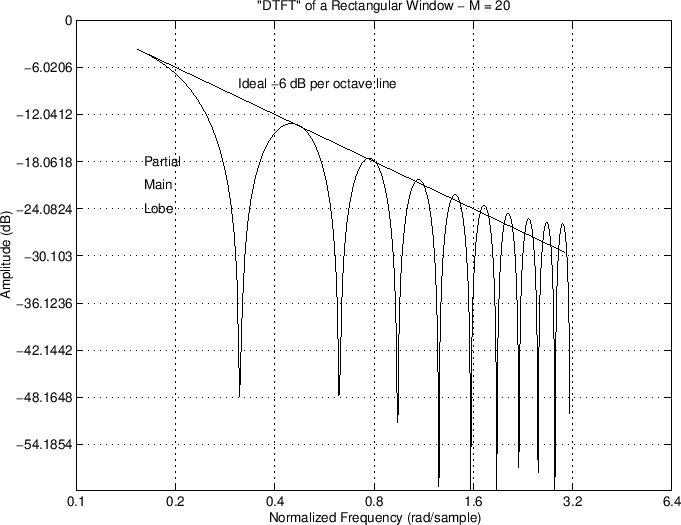
As the sampling rate approaches infinity, the rectangular window transform converges exactly to the sinc function. Therefore, the departure of the roll-off from that of the sinc function can be ascribed to aliasing in the frequency domain, due to sampling in the time domain.