Least-Squares Linear-Phase FIR Filter Design

Let the FIR filter length be $L+1$ samples, with $L$ even, and suppose we'll initially design it to be centered about the time origin (``zero-phase''). Then the frequency response is given on our frequency grid $\omega_k$ by

$$H(\omega_k) \eqsp \sum_{n=-L/2}^{L/2} h_n e^{-j\omega_kn}, \; k=0,1,2,\ldots,N-1, \; N\gg L.$$

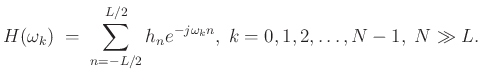
Enforcing even symmetry in the impulse response, i.e., $h_n = h_{-n}$ , gives a zero-phase FIR filter which we can later right-shift $L/2$ samples to make a causal, linear phase filter. In this case, the frequency response reduces to a sum of cosines:

$$\begin{eqnarray*} H( \omega_k ) &=& h_0 + 2\sum_{n=1}^{L/2} h_n \cos (\omega_k n), \quad k=0,1,2,\ldots, N-1, \end{eqnarray*}$$

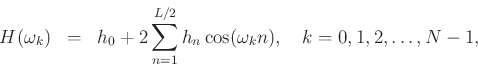
or in matrix form:

$$\left[ \begin{array}{c} H(\omega_0) \\ H(\omega_1) \\ \vdots \\ H(\omega_{N-1}) \end{array} \right] = \underbrace{\left[ \begin{array}{ccccc} 1 & 2\cos(\omega_0) & \dots & 2\cos[\omega_0(L/2)] \\ 1 & 2\cos(\omega_1) & \dots & 2\cos[\omega_1(L/2)] \\ \vdots & & & \\ 1 & 2\cos(\omega_{N-1}) & \dots & 2\cos[\omega_{N-1}(L/2)] \end{array} \right]}_A \underbrace{\left[ \begin{array}{c} h_0 \\ h_1 \\ \vdots \\ h_{L/2} \end{array} \right]}_x$$

Note that Remez exchange algorithms are also based on this formulation internally, but now $L\ll N$ .