Element Reflectance

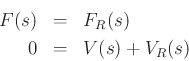
Imposing physical continuity constraints across the junction:

$$\begin{eqnarray*} F(s) &=& F_R(s)\\ 0 &=& V(s) + V_R(s) \end{eqnarray*}$$

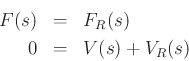
with

$$\begin{eqnarray*} F(s) &=& F^+(s) + F^-(s)\\ F_R(s) &=& F_R^+(s) + F_R^-(s)\\ V(s) &=& V^{+}(s)+V^{-}(s) =\frac{F^{+}(s)}{R_0} - \frac{F^{-}(s)}{R_0}\\ V_R(s) &=& V^{+}_R(s)+V^{-}_R(s) = \left[\frac{F^{+}_R(s)}{R(s)} - \frac{F^{-}_R(s)}{R(s)}\right] \end{eqnarray*}$$

we obtain the reflection transfer function (``reflectance'') of the element with impedance $R(s)$ :

$$\fbox{$\displaystyle S_R(s) \isdef \frac{F^{-}(s)}{F^{+}(s)} = \frac{R(s)-R_0}{R(s)+R_0}$}$$

This is the impedance step over the impedance sum, the usual force-wave reflectance at an impedance discontinuity, but now in the Laplace domain.