Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The optimal least-squares amplitude estimate may be found by the
following steps:
- Multiply the data
 by
by
 to zero the known phase
to zero the known phase 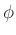
- Take the DTFT of the
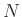 samples of
samples of  , suitably zero padded, and evaluate
it at the known frequency
, suitably zero padded, and evaluate
it at the known frequency 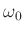
- Discard any imaginary part since it can only contain noise
- Divide by
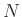 to obtain a true coefficient of projection onto
the sinusoid
to obtain a true coefficient of projection onto
the sinusoid
 (Method 3)
(Method 3)
Amplitude and Phase Estimation
Multiplying the optimal amplitude estimator by 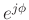 suggests
the following generalization for including phase:
suggests
the following generalization for including phase:
That is,
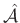 is given by the complex coefficient of
projection of
is given by the complex coefficient of
projection of  onto the complex sinusoid
onto the complex sinusoid
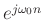 at the known
frequency
at the known
frequency 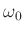 .
.
Proof by the orthogonality principle (Method 3):
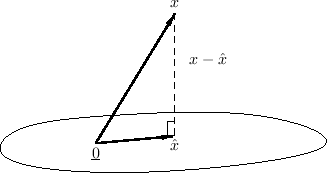
The orthogonality principle for linear least squares estimation states
that
That is, if 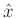 is our optimal signal model (viewed now as an
is our optimal signal model (viewed now as an
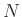 -vector in
-vector in
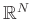 ), then we must have
), then we must have
Thus, the complex coefficient of projection of  onto
onto
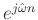 is given by
is given by
The optimality of
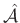 in the least squares sense follows from the
least-squares optimality of orthogonal projection.
in the least squares sense follows from the
least-squares optimality of orthogonal projection.
Frequency Estimation
The preceding cases suggest the following sinusoidal frequency estimator:
That is, the sinusoidal frequency estimate is defined as that
frequency which maximizes the DTFT magnitude.
- Given this frequency, the least-squares sinusoidal amplitude and phase
estimates are given by
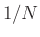 times the DTFT evaluated at that
frequency
times the DTFT evaluated at that
frequency
- It can be shown that this is the optimal least-squares estimator
for a single sinusoid in white noise
- If the additive white noise is Gaussian, then it is also the
maximum likelihood estimator
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
[Comment on this page via email]
![$\displaystyle \zbox{\hat{A}= \frac{1}{N}\mbox{re}\left\{\hbox{\sc DTFT}_{\omega_0 }\left[e^{-j\phi} x\right]\right\}}
$](img117.png)
![$\displaystyle \zbox{\hat{A}= \frac{1}{N}\mbox{re}\left\{\hbox{\sc DTFT}_{\omega_0 }\left[e^{-j\phi} x\right]\right\}}
$](img117.png)
 (Method 3)
(Method 3)
![]() suggests
the following generalization for including phase:
suggests
the following generalization for including phase:

![]() is our optimal signal model (viewed now as an
is our optimal signal model (viewed now as an
![]() -vector in
-vector in
![]() ), then we must have
), then we must have
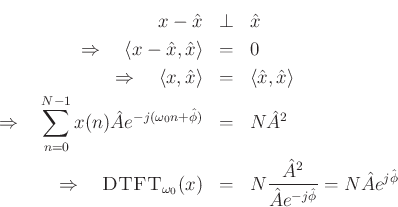
![]() onto
onto
![]() is given by
is given by