Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Boundary conditions:
Expand into Traveling-Wave Components:
Solving for outgoing waves gives
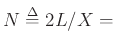 round-trip propagation time in samples
round-trip propagation time in samples
Subsections
Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download SimpleStrings.pdf
Download SimpleStrings_2up.pdf
Download SimpleStrings_4up.pdf
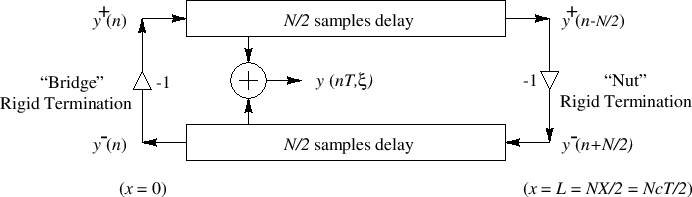

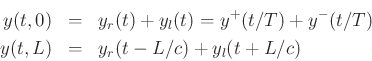
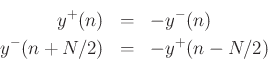
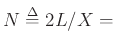 round-trip propagation time in samples
round-trip propagation time in samples