FFT Convolution

The convolution theorem $h*x \leftrightarrow H \cdot X$ shows us that there are two ways to perform circular convolution.

• direct calculation of the summation $= {\cal O}(N^2)$
• frequency-domain approach $= {\cal O}(N$   lg$N)$
  • Fourier Transform both signals
  • Perform term by term multiplication of the transformed signals
  • Inverse transform the result to get back to the time domain

Remember ... this still gives us cyclic convolution

Idea: If we add enough trailing zeros to the signals being convolved, we can get the same results as in acyclic convolution (in which the convolution summation goes from $m=0$ to $\infty$ ).

Question: How many zeros do we need to add?

• If we perform an acyclic convolution of two signals, $x$ and $h$ , with lengths $N_x$ and $N_h$ , the resulting signal is length $N_y = N_x + N_h - 1$ .

• Therefore, to implement acyclic convolution using the DFT, we must add enough zeros to $x$ and $y$ so that the cyclic convolution result is length $N_y$ or longer.
  • If we don't add enough zeros, some of our convolution terms ``wrap around'' and add back upon others (due to modulo indexing).
  • This can be called time domain aliasing.

• We typically zero-pad even further (to the next power of 2) so we can use the Cooley-Tukey FFT for maximum speed

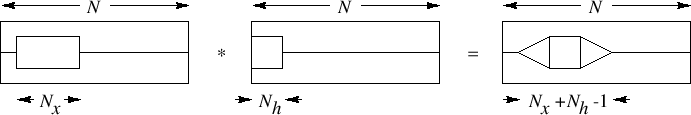
A sampling-theorem based insight:

Zero-padding in the time domain results in more samples (closer spacing) in the frequency domain. This can be thought of as a higher `sampling rate' in the frequency domain. If we have a high enough frequency-domain sampling rate, we can avoid time domain aliasing.