Let ![]() = impulse response of
= impulse response of ![]() th system pole. Then
th system pole. Then
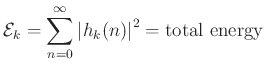
Thus, total energy is proportional to decay time.
To compensate, Jot proposes a tonal correction filter ![]() for the late reverb (not the direct signal).
for the late reverb (not the direct signal).
First-order case:
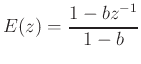
where
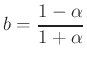
and
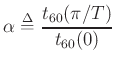
as before.