Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
High-Frequency Damping Lowpass:
For  at ``HF Damping'' frequency
at ``HF Damping'' frequency 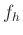 to be half of
middle-band
to be half of
middle-band  (gain
(gain 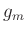 ), we require
), we require
Squaring and normalizing yields a quadratic equation:
Solving for 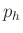 using the quadratic formula yields
using the quadratic formula yields
where
Discard unstable solution

To ensure  , GUI keeps middle-band
, GUI keeps middle-band  finite
finite
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Reverb.pdf
Download Reverb_2up.pdf
Download Reverb_4up.pdf
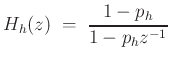
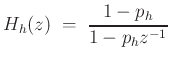
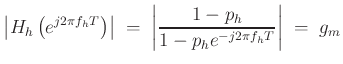
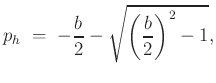
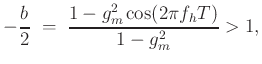
![]() , GUI keeps middle-band
, GUI keeps middle-band ![]() finite
finite