A Peek at Stability of Finite Difference Schemes

Let's look again at the difference scheme we derived for the 1-D wave eq, with the special time/space step $c=T/\Delta$ :

$$\begin{eqnarray*} u_{k}^{n+1} = u_{k-1}^{n}+u_{k+1}^{n}-u_{k}^{n-1} \end{eqnarray*}$$

The velocity sample $u(k,n)$ is a two-dimensional sequence with a time index and a spatial coordinate index.

Suppose we now take the DTFT with respect to the spatial index $k$ :

$$\begin{eqnarray*} \sum_{k=-\infty}^{\infty}u_{k}^{n+1}e^{-j\omega k\Delta} = \sum_{k=-\infty}^{\infty}(u_{k-1}^{n}+u_{k+1}^{n}-u_{k}^{n-1})e^{-j\omega k\Delta} \end{eqnarray*}$$

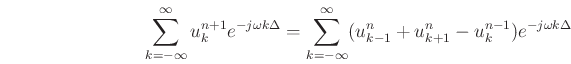
or

$$\begin{eqnarray*} U^{n+1}(\omega)= (e^{-j\omega\Delta}+e^{j\omega\Delta})U^{n}(\omega)-U^{n-1}(\omega) \end{eqnarray*}$$

where here $U^{n}(\omega)$ is the spatial spectrum of the solution at time $n$ , and $\omega$ is the spatial frequency variable. We can also write this in vector form as:

$$\begin{eqnarray*} \left[\begin{array}{c} U^{n+1}(\omega) \\ [2pt] U^{n}(\omega) \end{array}\right] &=& \left[\begin{array}{cc} 2\cos\omega\Delta & -1 \\ [2pt] 1 & 0 \end{array}\right] \left[\begin{array}{c} U^{n}(\omega) \\ [2pt] U^{n-1}(\omega) \end{array}\right] \end{eqnarray*}$$

Note that the state of the system is completely determined by $U^n(\cdot)$ and $U^{n-1}(\cdot)$ .