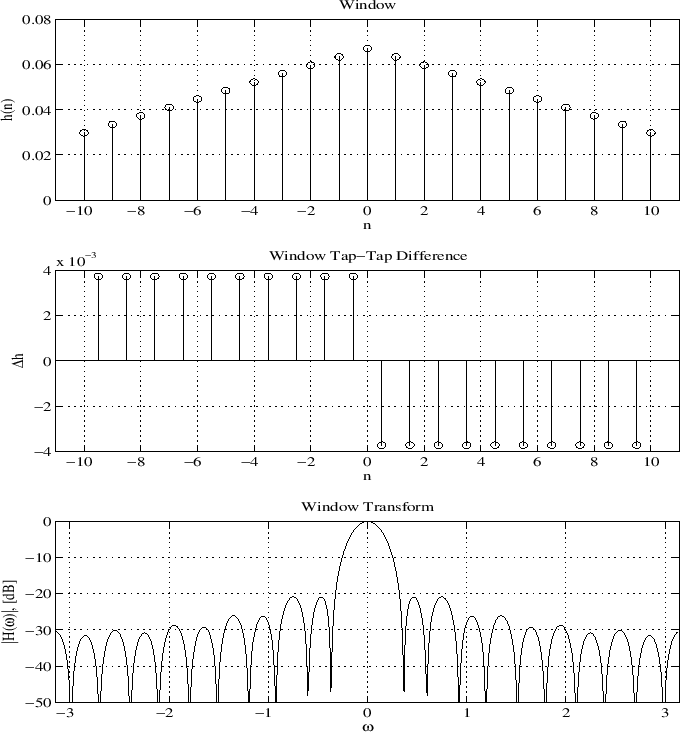
We can add a smoothness objective by adding
![]() -norm of the
first-order difference to the objective function.
-norm of the
first-order difference to the objective function.
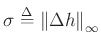 and set up
the inequality constraints
and set up
the inequality constraints
In matrix form:
![$\displaystyle \left[\begin{array}{c}
-\mathbf{D}\\
\mathbf{D}\end{array}\right]h-\sigma \mathbf1$](img61.png) |
Chebyshev norm of diff(h) added to the objective function
to be minimized (![]() ):
):
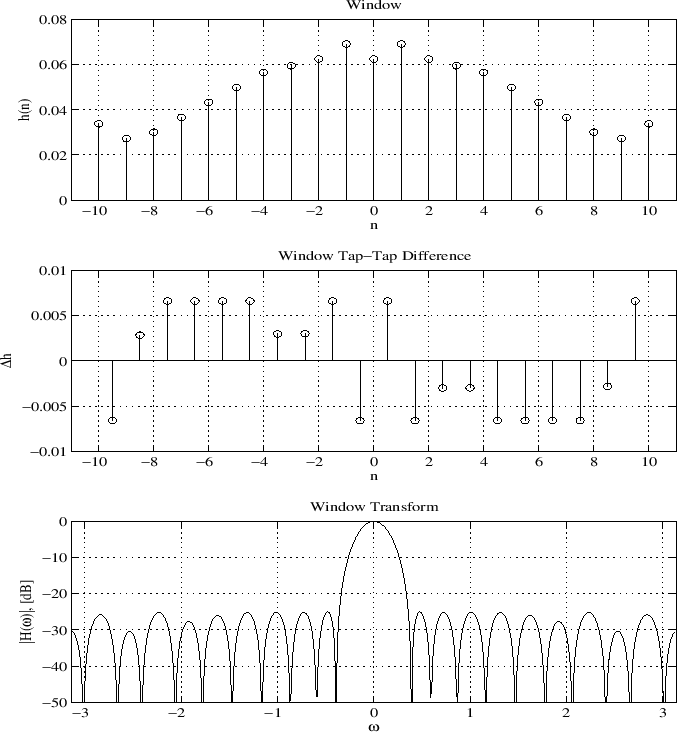
Twenty times the Chebyshev norm of diff(h) added to the objective function
to be minimized (![]() ):
):