Polyphase Haar Example

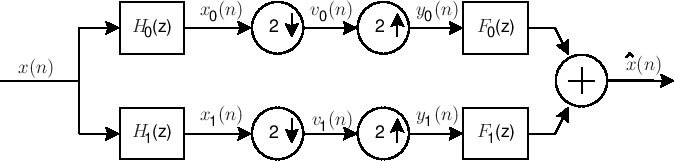
Let's look at the polyphase representation for this example. Starting with the filter bank and its reconstruction,

the polyphase decomposition of $H_0(z)$ is

$$H_0(z) = E_0(z^2) + z^{-1}E_1(z^2) = \frac{1}{2}+\frac{1}{2}z^{-1}$$

Thus, $E_0(z^2)=E_1(z^2)=1/2$ , and therefore

$$H_1(z) = 1-H_0(z) = E_0(z)-z^{-1}E_1(z)$$

We may derive polyphase synthesis filters as follows:

$$\begin{eqnarray*} {\hat X}(z) &=& \left[F_0(z)H_0(z) + F_1(z)H_1(z)\right] X(z)\\ &=& \left[\left(\frac{1}{2} + \frac{1}{2}z^{-1}\right)H_0(z) + \left(-\frac{1}{2}+\frac{1}{2}z^{-1}\right)H_1(z)\right]\\ &=& \frac{1}{2}\left\{\left[H_0(z)-H_1(z)\right] + z^{-1}\left[H_0(z) + H_1(z)\right]\right\} \end{eqnarray*}$$

The polyphase representation of the filter bank and its reconstruction can now be drawn as below:

Notice that the reconstruction filter bank is formally the transpose of the analysis filter bank.

Commuting the downsamplers (by the noble identities), we obtain

Since $E_0(z)=E_1(z)=1/2$ , this is simply the OLA form of an STFT filter bank for $N=2$ , with $N=M=R=2$ , and rectangular window $w=[1/2,1/2]$ . That is, the DFT size, window length, and hop size are all 2, and both the DFT and its inverse are simply sum-and-difference operations.