Haar Example

Before we leave this case (amplitude-complementary, two-channel, critically sampled, perfect reconstruction filter banks), let's see what happens when $H_0(z)$ is the simplest possible lowpass filter having unity dc gain, i.e.,

$$H_0(z) = \frac{1}{2} + \frac{1}{2}z^{-1}$$

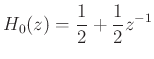
This case is obtained above by setting $E_0(z^2)=1/2$ , $o=1$ , and $h_0(1)=1/2$ .

The polyphase components of $H_0(z)$ are clearly

$$E_0(z^2)=E_1(z^2)=1/2.$$

Choosing $H_1(z)=1-H_0(z)$ and choosing $F_0(z)$ and $F_1(z)$ for aliasing cancellation, the four filters become

$$\begin{eqnarray*} H_0(z) &=& \frac{1}{2} + \frac{1}{2}z^{-1} = E_0(z^2)+z^{-1}E_1(z^2)\\ [0.1in] H_1(z) &=& = 1-H_0(z) = \frac{1}{2} - \frac{1}{2}z^{-1} = E_0(z^2)-z^{-1}E_1(z^2)\\ [0.1in] F_0(z) &=& H_1(-z) = \frac{1}{2} + \frac{1}{2}z^{-1} = H_0(z)\\ [0.1in] F_1(z) &=& -H_0(-z) = -\frac{1}{2} + \frac{1}{2}z^{-1} = -H_1(z) \end{eqnarray*}$$

Thus, both the analysis and reconstruction filter banks are scalings of the familiar Haar filters (``sum and difference'' filters $(1\pm z^{-1})/\sqrt{2}$ ).

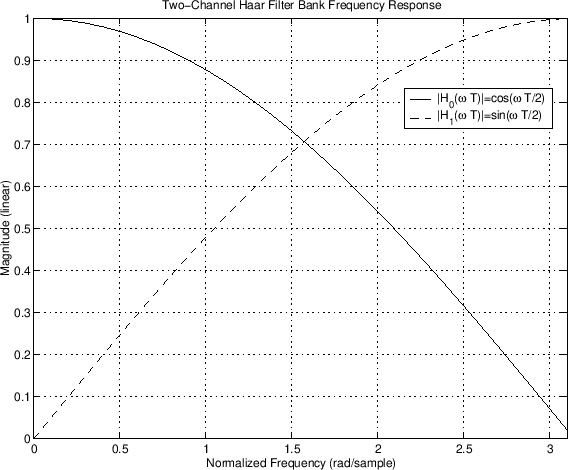
The frequency responses are

$$\begin{eqnarray*} H_0(e^{j\omega}) &=& \quad\,F_0(e^{j\omega}) = \frac{1}{2} + \frac{1}{2}e^{-j\omega}= e^{-j\frac{\omega}{2}} \cos\left(\frac{\omega}{2}\right)\\ [0.1in] H_1(e^{j\omega}) &=& -F_0(e^{j\omega}) = \frac{1}{2} - \frac{1}{2}e^{-j\omega}= j e^{-j\frac{\omega}{2}} \sin\left(\frac{\omega}{2}\right) \end{eqnarray*}$$

which are plotted below: