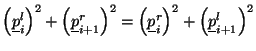Power Conservation at Scattering Junctions

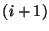At the junction between the $i$th and $(i+1)$th tubes, the continuity relations (1.5), when multiplied together, imply that

$$p_{i}u_{i} = p_{i+1}u_{i+1}$$

This is simply a statement of conservation of power at the interface. Using the definitions of traveling wave variables from (1.6), we then have that

$$\left(p_{i}^{l}+p_{i}^{r}\right)Y_{i}\left(p_{i}^{l}-p_{i}^{r}\ri... ...\left(p_{i+1}^{l}+p_{i+1}^{r}\right)Y_{i+1}\left(p_{i+1}^{l}-p_{i+1}^{r}\right)$$

or, rearranging terms,

$$Y_{i}\left(p_{i}^{l}\right)^{2} + Y_{i+1}\left(p_{i+1}^{r}\right)^{2} = Y_{i}\left(p_{i}^{r}\right)^{2} + Y_{i+1}\left(p_{i+1}^{l}\right)^{2}$$

In other words, the sum of the squares of the incident waves, weighted by their respective tube admittances, is equal to the same weighted square sum of the reflected waves. Assuming that the 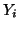$Y_{i}$ are positive, then, a weighted 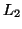$L_{2}$ measure of the signal variables (pressure waves) is preserved through the scattering operation. This reflects the inherent losslessness of the tube interface.

In terms of the power-normalized variables defined by (1.9), and scattered according to (1.10), we will have (due to the orthogonality of the scattering matrix),

$$\left(\underline{p}_{i}^{l}\right)^{2} + \left(\underline{p}_{i+1... ...eft(\underline{p}_{i}^{r}\right)^{2} + \left(\underline{p}_{i+1}^{l}\right)^{2}$$

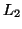Thus the $L_{2}$ norms of the incident and reflected vectors of power-normalized wave variables are the same.