


Next: Signal and Coefficient Quantization
Up: Adaptors
Previous: Adaptors
The adaptor equations for a connection of 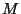 ports, in either the series (2.31) or parallel (2.32) case, may be written as
ports, in either the series (2.31) or parallel (2.32) case, may be written as
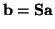 |
(2.37) |
where
![$ {\bf b} = [b_{1}, \hdots , b_{M}]^{T}$](img388.png) and
and
![$ {\bf a} = [a_{1}, \hdots , a_{M}]^{T}$](img389.png) , and where we have
, and where we have
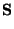 |
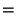 |
|
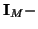 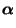  |
|
Series adaptor (voltage waves) |
(2.38) |
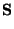 |
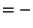 |
|
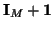 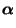  |
|
Parallel adaptor (voltage waves) |
(2.39) |
Here 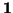 is an
is an 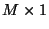 vector containing all ones,
vector containing all ones,
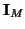 is the
is the 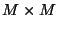 identity matrix, and
identity matrix, and 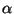
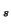 and
and 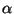
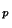 are defined by
are defined by
The sum of the elements of either 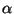
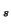 or
or 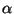
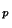 is 2.
For power wave variables, we have a similar relationship,
is 2.
For power wave variables, we have a similar relationship,
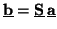 |
(2.40) |
where
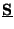 |
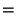 |
|
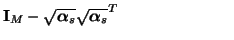 |
|
Series adaptor (power-normalized waves) |
|
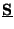 |
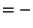 |
|
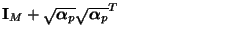 |
|
Parallel adaptor (power-normalized waves) |
|
Here the square root sign indicates an entry-by-entry square root of a vector (all entries of 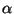
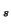 and
and 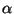
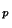 are non-negative).
are non-negative).
Defining the Euclidean norm of a column vector 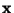 as
as
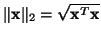 , it is easy to show that a power normalized scattering matrix
, it is easy to show that a power normalized scattering matrix
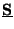 is norm-preserving in either the series or parallel case, i.e., we have
is norm-preserving in either the series or parallel case, i.e., we have
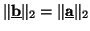 |
(2.41) |
For voltage waves, we have the preservation of a weighted 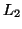 norm, i.e.,
norm, i.e.,
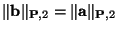 |
(2.42) |
where
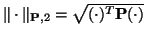 ; in this case,
; in this case, 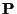 is an
is an 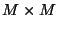 positive definite diagonal matrix simply given by diag
positive definite diagonal matrix simply given by diag
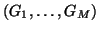 . It should be clear that (2.41) and (2.42) are merely re-statements of power conservation at a memoryless, lossless
. It should be clear that (2.41) and (2.42) are merely re-statements of power conservation at a memoryless, lossless 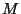 -port.
-port.
Note that multiplying 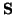 or
or
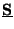 by a vector requires, in either the series of parallel case,
by a vector requires, in either the series of parallel case, 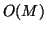 adds and multiplies; in particular, it is cheaper than a full
adds and multiplies; in particular, it is cheaper than a full 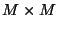 matrix multiply.
matrix multiply.



Next: Signal and Coefficient Quantization
Up: Adaptors
Previous: Adaptors
Stefan Bilbao
2002-01-22
![]() ports, in either the series (2.31) or parallel (2.32) case, may be written as
ports, in either the series (2.31) or parallel (2.32) case, may be written as
![]() as
as
![]() , it is easy to show that a power normalized scattering matrix
, it is easy to show that a power normalized scattering matrix
![]() is norm-preserving in either the series or parallel case, i.e., we have
is norm-preserving in either the series or parallel case, i.e., we have
![]() or
or
![]() by a vector requires, in either the series of parallel case,
by a vector requires, in either the series of parallel case, ![]() adds and multiplies; in particular, it is cheaper than a full
adds and multiplies; in particular, it is cheaper than a full ![]() matrix multiply.
matrix multiply.