Fitting Filters in Matlab

1. Measure the decay rate of each partial overtone, and calculate the desired amplitude response for the loop filter in a digital waveguide model. Take the EDR, and using the rate of decay of the signal, compute the necessary gains for the harmonic series of the signal. We will have code samples for fitting a line to the dB decay of one frequency in a later section.

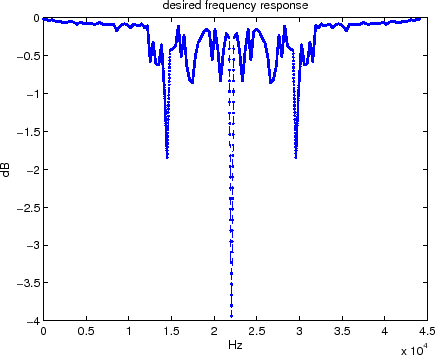
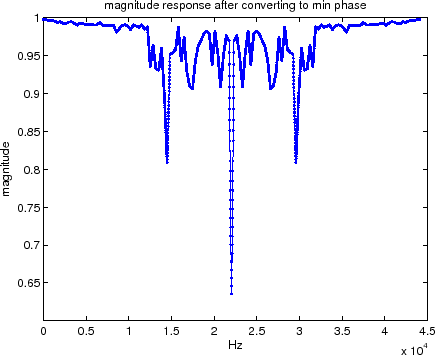
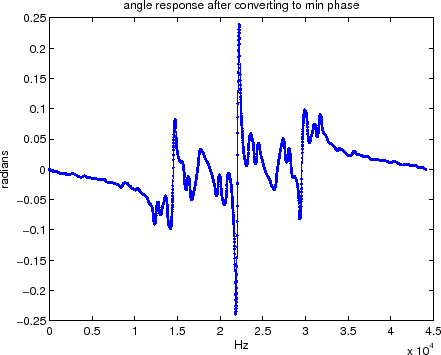
   Figure 4 shows the resulting desired magnitude response of our loop filter as calculated from the EDR..

   Figure 4: Desired magnitude response of our loop filter.

   

2. Convert the desired amplitude response to minimum-phase form. This simplifies complex behavior involving the phase of the excitation signal with the fitted filter. Figure 5 shows the magnitude response after converting to minimum phase.

   Figure 5: The desired magnitude response after converting to minimum phase

   
   Figure 6 shows the resulting minimum-phase response.

   Figure 6: The phase response after converting to minimum phase.

   

3. Design the loop filter to approximate the minimum-phase frequency response. Figure 7 shows the result obtained for this example using invfreqz in Matlab (or Octave Forge).

   Figure 7: Magnitude and Phase responses of the fitted filter using invfreqz

   

   The code segments demonstrates how we fitted a filter using invfreqz and stmcb.

   % Note that Hmin corresponds to the response of the min-phase filter
   % that we want to fit to obtain filter parameters using invfreqz
   wH = (0:Npt/2)*2*pi/Npt;
   wH(1) = wH(2);
   wt = 1./wH;
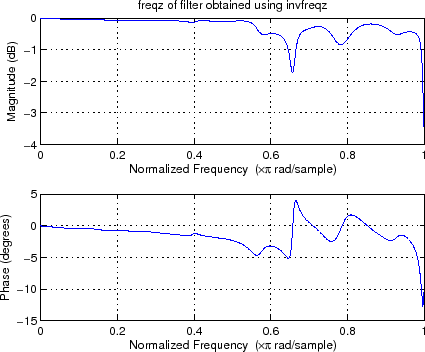
   [B,A] = invfreqz(Hmin(1:Npt/2+1),wH,25,25,wt);
   figure;freqz(B,A)
   title('freqz of filter obtained using invfreqz');
   
   % % Obtain filter parameters using stmcb
   hdesired = real(ifft(Hmin));
   figure;plot((0:length(hdesired)-1)/fs,(hdesired));
   title('impulse response of min phase filter')
   xlabel('seconds');
   ylabel('amplitude');
   [stmb,stma] = stmcb(hdesired,40,40);
   figure;freqz(stmb,stma)
   title('freqz of filter obtained using stmcb');
   

   Figure 8 shows the result obtained for this example using stmcb from the Matlab Signal Processing Tool Box.

   Figure 8: Magnitude and phase response of the filter

   

   Plotting the results in Matlab is simple, as the following code segments shows. Note that Matlab's freqz function takes as arguments the coefficients of a filter plots the magnitude and phase responses of the described filter.

   figure;freqz(B,A)
   title('freqz of filter obtained using invfreqz');
   
   figure;freqz(stmb,stma)
   title('freqz of filter obtained using stmcb');