Computing the Excitation Signal

Now that we have a string-model for our guitar model, we can use it along with the original recorded guitar tone to compute the excitation signal using inverse-filtering.

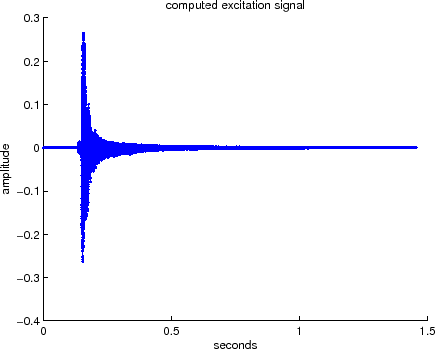
1. Inverse filter to obtain the excitation signal. Here we make critical assumptions. 1) the excitation signal can be removed from the original signal and 2) that this excitation signal when fed into a filtered loop will respond as the original signal did. Therefore, in order to obtain the excitation signal, we delay the original signal, run it through our filter, and subtract the resulting signal from the original to obtain the excitation signal. 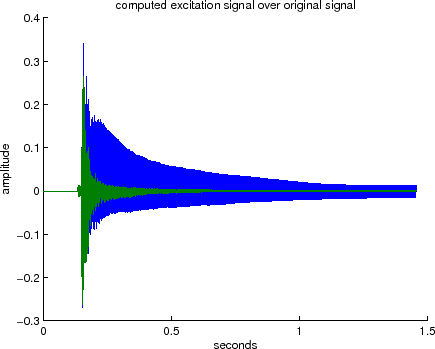Figure 11 shows the result obtained for this example.

   Figure 11: Plot of the computed excitation signal over the original signal

   

   The following code segment computes the excitation signal and writes it out to disk.

   % find the excitation signal. 
   % FUND_F corresponds to the fundamental freq
   N = round(fs/FUND);
   
   del_y = [zeros(N,1);y(1:end-N)];
   filt_y = filter(stmb,stma,del_y);
   % filt_y = filter(B,A,del_y);
   
   e_sig = y-filt_y;
   wavwrite(e_sig,fs,bits,'../sound_files/e_sig.wav');
   

2. The resulting excitation signal is ploted in Figure 12.

   Figure 12: Computed excitation signal

   

3. Figure 13 shows the resulting excitation signal in dB.

   Figure 13: Computed excitation signal in dB