Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Two-Zero String Damping Filter
A disadvantage of the decay-stretching parameter is that it affects
tuning, except when 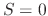 . This can be alleviated by going to a
second-order, symmetric, linear-phase FIR filter having a transfer
function of the form [19]
. This can be alleviated by going to a
second-order, symmetric, linear-phase FIR filter having a transfer
function of the form [19]
Due to the symmetry of the impulse response
![$h_d=[g_1,g_0,g_1,0,0,\ldots]$](img50.png) about time
about time 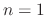 , only two multiplies
and two additions are needed per sample. The previous one-zero
loop-filter required one multiply and two additions per sample.
Since the delay is equal to one sample at all frequencies (in the
needed coefficient range), we obtain tuning invariance for the price
of one additional multiply per sample. We also obtain a bit more
lowpass filtering. Listening to both cases, one might agree that the
one-zero loop filter has a ``lighter, sweeter'' tone than the two-zero
case. In general, the tone is quite sensitive to the details of all
filtering in the feedback path of Fig.4.
, only two multiplies
and two additions are needed per sample. The previous one-zero
loop-filter required one multiply and two additions per sample.
Since the delay is equal to one sample at all frequencies (in the
needed coefficient range), we obtain tuning invariance for the price
of one additional multiply per sample. We also obtain a bit more
lowpass filtering. Listening to both cases, one might agree that the
one-zero loop filter has a ``lighter, sweeter'' tone than the two-zero
case. In general, the tone is quite sensitive to the details of all
filtering in the feedback path of Fig.4.
See
[14]
for a derivation of the FIR filter coefficients
h0,h1 as a function of brightness B. A Faust implementation may then be written as follows:
t60 = hslider("decaytime_T60", 4, 0, 10, 0.01); // sec
B = hslider("brightness", 0.5, 0, 1, 0.01); // 0-1
rho = pow(0.001,1.0/(freq*t60));
h0 = (1.0 + B)/2;
h1 = (1.0 - B)/4;
dampingfilter2(x) = rho * (h0 * x' + h1*(x+x''));
Subsections
Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Download faust_strings.pdf
![]() . This can be alleviated by going to a
second-order, symmetric, linear-phase FIR filter having a transfer
function of the form [19]
. This can be alleviated by going to a
second-order, symmetric, linear-phase FIR filter having a transfer
function of the form [19]